| English | Français |
At the macroscale, transport processes such as diffusion, viscosity, or heat conduction are described in terms of macroscopic equations involving phenomenological coefficients as it is the case. These nonequilibrium macroscopic properties emerge from the microscopic motion of the atoms and molecules composing matter. A huge gap separates the micro- from the macroscale, which can be bridged thanks to appropriate stochastic descriptions holding at mesocopic scales and allowing us to derive exact expressions for the transport coefficients.
|
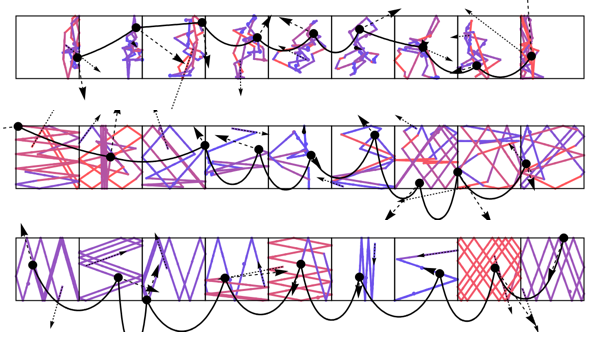
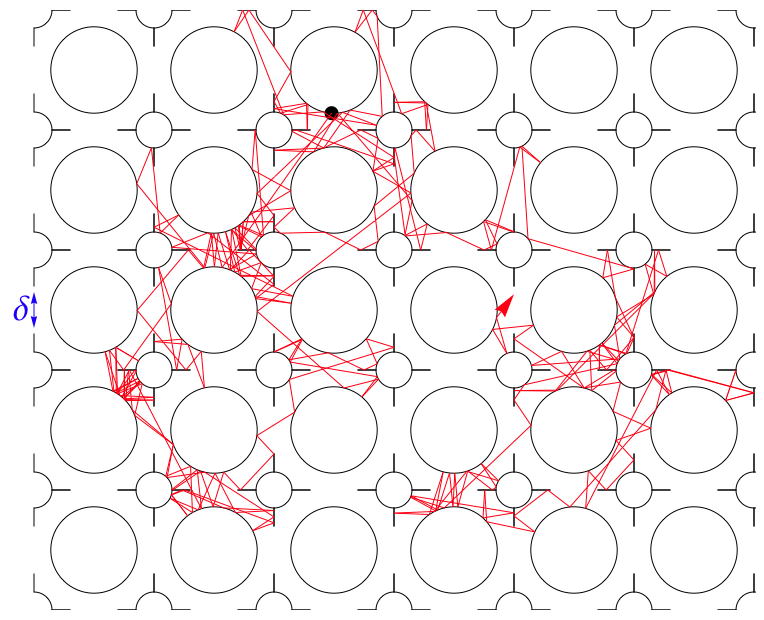
Selected publications Microscopic derivation of Fourier’s law: Heat conduction and Fourier's law in a class of many particle dispersing billiards, Heat conductivity from molecular chaos hypothesis in locally confined billiard systems, Green-Kubo and Einstein-Helfand methods for molecular dynamics: Transport and Helfand moments in the Lennard-Jones fluid. I. Shear viscosity, Deterministic diffusions: Persistence effects in deterministic diffusion, Nonlinear transport: Nonlinear diffusion from Einstein's master equation, |
|
 |
|
 |
|
 |